PLATÓN Y LA PRIMERA DESCRIPCIÓN DE UNA TEMPERACIÓN* EN NUESTRA CULTURA (hipótesis para su exposición):

Hipótesis arqueológica sobre las primeras temperaciones y escalas musicales (capítulo 3)

.
NOTA* EN EL TÍTULO: Como encabezamiento a estos artículos, explicamos que en nuestros trabajos hemos utilizado las palabras "temperación" y "temperar" -tal como seguiremos haciendo- . Habida cuenta que la voz "temperamento", comunmente usada para describir el acto de calcular los intervalos en la afinación, se ha declinado a modo "italiano" y sin conjugaciones españolas. De tal manera, concibo personalmente que aquel término "italianizante" con el que se describe la búsqueda armónica de la escala y en el que tan solo se admite la palabra "temperamento"; ha de traducirse al castellano por "temperar", "temperación" y etc.. Puesto que el acto de analizar los "temperamentos" de la música, ha de ser descrito y conjugado como "temperar"; a la vez que el nombre su verbo sería "la temperación".
.

.
.
SOBRE ESTAS LINEAS: El filósofo Pitágoras; padre de las teorías sobre la "Armonia Mundi" en Occidente. Nacido en Samos en el siglo VI a.C., isla jonia sita en el paso entre Oriente Medio y Europa. Viviría en el entorno de marinos; quienes precisaban del estudio continuado y mejora en los cálculos y las matemáticas con el fin de guiar bien sus naves -dominando la situación de las estrellas, las horas y la orientación-. Formándose en este ambiente culto y rico, basado en el mercado marítimo y pleno de estudiosos; quienes durante las noches ampliarían sus conocimientos sobre la cúpula celeste. Posteriormente, su "biografía" (que en parte es fabulosa) narra que se traslada a zonas de Canaan o Israel, donde se inicia en cultos eremitas, para pasar más tarde a las de Egipto. Allí se supone que ingresó en un templo dedicado a la veneración solar; recintos de los que comunmente no podían salir los que aceptaban integrarse en su comunidad. Creyendo la Historia que quienes "escapaban" de esos santuarios nilotas, eran perseguidos severamente bajo el signo de la apostatía -tal como sucede comunmente con los votos sacros, en las religiones-.
.

Por lo demás y en lo que se refiere a estos sacerdotes o funcionarios del Nilo, se sabe con certeza que eran educados con esmero, pero no podían revelar los secretos de importancia aprendidos en el culto, en su filosofía y en el templo. Todo lo que era común hasta hace apenas unos siglos y que obligaba guardar los secreto a los "iniciados", con el fin de que esos conocimientos no cayeran en manos enemigas o de ajenos al poder -faraónico en este caso-. De hecho, parece ser que los novicios y quienes estudiaban en las llamadas "casas de la vida" nilotas (similares a nuestras universidades o seminarios), juraban no desvelar ni transmitir lo aprendido a terceros -fuera de los recintos sagrados-, sin el consentimiento de sus superiores. Una fórmula basada en el secretismo que durante la Antigüedad fue un hecho radicalmente cierto y por el cual algunas civilizaciones se hallaban en una superioridad plena, debido a que jamás enseñaban los procedimientos de progreso. Todo lo que -de alguna forma- perdura hasta La Ilustración en nuestras Sociedades; cuando en el siglo XVIII, por primera vez se permite divulgar y publicar libremente los conocimientos. Sin control por parte de las autoridades y con el fin de que las profesiones no continuasen pasando de padres a hijos -aunque sobre todo, para que los conocimientos de ciencia o física ya no se sometieran a la censura plena de un estamento, que hasta La Ilustración los regulaba y dirigía de forma "secreta", dogmática y autoritaria-.
.
Pese a lo que narramos y regresando a nuestro filósofo, parece ser que Pitágoras logró salir del templo egipcio a consecuencia de la invasión asiria del Nilo. Un reino que se ve azotado por Cambises II, quien avanzó sobre ellos a cuenta de un "desplante" del faraón cuando se niega a envíarle una hija suya como esposa (por conocer que los aqueménides destinaban al harén de las concubinas reales a toda aquella que no fuera de sangre persa). Siendo así, narra la leyenda que Pitágoras vivió el asedio de Cambises y que se libró de la muerte que el tirano rey de Mesopotamia daba a los sacerdotes del faraón, por ser extranjero. Asimismo, la "biografía" (fabulosa) que redactan sus seguidores y "admiradores", cuenta que trás salir del templo, es "enviado" a Babilonia como rehén. Aunque al poco tiempo de llegar a esa tierra, el tirano Cambises -que estaba guerreando en el Nilo- fue derrocado por un mago, quien usurpa la figura del hermano del rey. Siendo así y divulgándose la historia entre los persas de que Cambises había matado a su propio hermano para ocupar el trono; las revueltas no cesaron, hasta que el país aqueménide quedó en manos de aquel brujo. Creyendo los "biógrafos" de Pitágoras que durante este tiempo el "iniciado" en Egipto, aprovecha también la estancia en Babilonia para estudiar su matemática y astronomía, ampliar conocimientos y entablar amistad con aquellos que por entonces gobernaban el reino (los sacerdotes y magos). Finalmente, se sabe con certeza que regresó a su Samos natal, donde se establece "una sociedad" con el fin de enseñar el cúmulo de conocimientos recogidos a lo largo de sus viajes y durante su "dilatada" vida -lo que había estudiado en Canaan, en los templos de Egipto y entre los augures babilonios-.
.
En o que se refiere al relato de su vida, no sabemos si aquella historia del sabio de Samos recoge la de varios personajes en uno. O bien, si se construye de esta forma "su biografía", con el fin de narranos y explicar el origen de los conocimientos que el filósofo enseñaba y difundió. Sea como fuere, el pitagorismo se establece como "un grupo" (o secta) que escogía "ciertos elegidos" para formarlos en unos valores y unos conocimientos comunes; pero que no permitía la divulgación "gratuita" -o plenamente abierta- de sus ideas. Menos aún, la del llamado "dogma"; un secreto fundamental que promulgó el sabio, relacionando la música con la física y ambas, con el Cosmos, sus fuerzas y sus leyes. Enseñando primeramente a "temperar", buscando la escala trás conocer el significado y valores numéricos de cada nota. Para más tarde pasar a comprender que la afinación y la armonía tenía una relación con el Universo. Tanta que consideraban que las estrellas y los planetas estaban unidos -o sustentados en el vacío- y giraban en el Cosmos, atendiendo a unas normas físicas relacionadas con las de los temperamentos. Es decir, en que la escala musical se contenían los secretos del Universo, los de la Creación y los del "número perfecto". Una cifra pitagórica, que compone la esencia del Cosmos y que tal como el sabio griego nos la transmitió, todo hace pensar que claramente procede de conceptos egipcios muy anteriores; de ideas como el del Maat -la medida arquitectónica, la balanza y ponderales en el reino de Osiris y el peso del corazón (en el juicio final de los dioses)-. 
.
.
.
Es decir, que claramente en Pitágoras vemos el recuerdo -o la compilación- de los conocimientos religiosos del Nilo y de Mesopotamia, divulgados gracias al espíritu heleno. Una cultura griega, que permitía escribir y dar a conocer la sabiduría -sin grandes trabas ni temores a que la ciencia cayera a manos de ajenos al poder-. Teniendo la Hélade de hace mil quinientos años un espíritu similar al de la Europa del siglo XVIII, donde la sabiduría se admiraba y se permitió divulgarla (ya que el miedo a los conocimientos, tanto como su falta de difusión, provocan el estancamiento de las civilizaciones). Por todo ello, en la "supuesta biografía" del sabio, quizás se esconde el hecho de que la filosofía pitagórica fuera un elenco de las religiones milenarias de Egipto y de Mesopotamia, decantadas y recicladas por la escuela del filósofo griego durante el siglo VI a.C.. Cuando los jonios (conocidos viajeros y pensadores) consiguen compendiar y enseñar los conocimientos más destacados del Mundo en que viven y de las civilizaciones que les antecedieron.
.
Debido a todo lo antes narrado, entre los discípulos y seguidores de la escuela pitagórica se hallaban las élites de Grecia. Donde no podía faltar de algún modo, el aristócrata Platón; quién -al parecer- compra varios "libros" a los seguidores de Pitágoras con el fin de completar "sus ideas". Ejemplares desde los que Platón "se inspira" para describir los conocimientos que atribuye plenamente a su persona -aunque la realidad histórica parece que fue muy distinta (tal como se desprende del estudio de sus exposiciones acerca de la temperación)-. Por su parte y en base a aquellos escritos, durante el siglo XV y XVI, las Escuelas Neoplatónicas logran reavivar la conciencia filosófica, divulgando de nuevo gran parte de los conceptos de Platón. De todo cuanto surgen nuevos movimientos, que incorporados a las mejoras de la astronomía y de la matemática -en la Europa renacentista-, logran que el "Neoplatonismo" genere una filosofía aplicada al Cosmos. De aquellas teorías y de ese tiempo, nacieron astrónomos como Galileo y Kepler; quienes, partiendo desde teorías pitagóricas, consiguen cambiar el rumbo de la Historia de la ciencia. Un camino en el que se había retrocedido miles de años tras la "caida" de Grecia; ya que algunas escuelas helenas -como precisamente la jonia-, habían conseguido divulgar y enseñar incluso el heliocentrismo (junto a teorías como la "precesión de equinocios", o "la traslación" de la Tierra y etc).
.
Consecuentemente, ya en el siglo XV y de nuevo gracias a las enseñanzas platónicas, se generan nuevas tendencias entre las que el pitagorismo llega a inspirar a investigadores como Kepler; quien formula sus leyes en base a esta filosofía. De aquellos avances e ideas renacentistas, nacerá algún tiempo después, la matemática o la física ilustrada y en especial la astronomía y la ciencia de Newton: Un pitagórico en su más pura esencia, que buscaba en los conocimientos del Mundo Antiguo, la inspiración y fundamento para desarrollar su física y su saber. Todo cuanto logrará el gran genio inglés -cumbre de la sabiduría más sublime-; al aplicar las teorías de Pitágoras en su modo de investigar y de vivir, tanto como en la interpretación de la Naturaleza. Ya que -en mi opinión-, la matemática es una herramienta que puede demostrarse gracias a la física, pero a su vez la física es una "herramienta" que se muestra plenamente en el arte. Siendo así, las artes deben constituir la "herramienta" por la cual logremos mostrar lo bello y sublime en los conceptos matemáticos más puros. Un método para comprender ese ciclo cerrado entre matemática, física y artes; que es -a mi juicio- lo que habríamos de definir como "filosofía". En el que -por su parte-, las humanidades serían aquellas disciplinas que logran explicar y aplicar a la vida común (y en todos sus aspectos), los valores y conclusiones obtenidas al estudiar de modo anterior la ciencia y las artes.
.

.
COMENTARIO A LAS IMÁGENES: Tres párrafos antes (en el margen izquierdo y sobre estos), habíamos visto la efigie del pitagórico Isaac Newton en un sello de la República Soviética de 1987. Este físico y místico, ha sido en gran parte olvidado por la filosofía del Sur de Europa, tanto como por la ciencia centroeuropea. En el primer caso quizás porque en el Mediterráneo la unión de la física y la teología, o de la matemática y la mística; son un mundo que produce rechazo y hasta abominazción. Todo lo que se ha podido comprobar en situaciones como la del tristísimo Galileo (de algún modo, antecesor directo de Newton -como "colaborador" de Kepler-). Por su parte, el olvido en Centroeuropa del genio inglés, procede por no querer reconocer que se adelantó a Leibniz en muchos de sus aspectos; ya que Alemania tiene en su matemático y pensador, el "eje sobre el cual rota" La Ilustración. Sea como fuere, la diferencia entre Newton y los demás reside en que aunque sus teorías puedan superarse -o mejorarse-, el sentido filosófico de sus ideas y la belleza de su pensamiento, permanece. De ello se deduce que todo cuanto creó e ideó iba más allá de nuestro tiempo; porque cuando la ciencia halla una explicación que además está cargada de belleza, no solo ha encontrado la verdad, sino también su significado. Así -y en mi opinión- muchos de los que creen haber superado a Newton sufren el mismo mal que los que desearon superar a Bach: Desconocer que el genio, además de ser un hombre superdotado, sobre todo es un nexo con lo divino, lo elevado o trascendente. 
ARRIBA: Grabado del siglo XIX que representa a Cambises II a su regreso de Egipto, perdido con su ejército en el desierto (obra de Alfredo y Angelo Castiglioni -fuente de la que tomamos la imagen: Wikipedia, y esta a su vez, desde un artículo de El Pais 26 nov 2009).
.
.
1º) EL TIMAIOS DE PLATÓN:
.
Es conocido que en el Diálogo de Platón Timaios (31-36) se explica la afinación temperada planteando que la creación del Universo fué hecha a imagen y semejanza de la de "la música" y de sus notas (o viceversa). Este texto se tiene como la primera descripción de una forma de medir armónicamente una escala musical -al menos en Occidente-. En el cual nos narra Platón como el Demiurgo crea el Cosmos y en el fragmento 35 explica el "nacimiento y concepción" del "todo", de foma exacta a la de una "temperación" musical. De tal manera y como si los siete planetas fueran las siete notas, junto a sus ciclos calendáricos (con sus ritmos y melodías, a modo del giro armónico de los astros), uniendo así Platón el Cosmos a la música.
.
Para el estudio de estos fragmentos, analizaremos en primer lugar las partes del Diálogo que preceden a la mención de la afinación. Tras ello, pasaremos al "párrafo 35", donde el filósofo ya trata acerca de la división del Cosmos en la misma forma que el de las notas musicales (la traducción del Timaios que manejamos, presentada por Pérez Martel - en edición de Alianza Ed. Madrid 2004- es de I.Burnet ,Oxford 1903; en ella el autor habla "del dios creador", pero al ser un "Dios" en concepto platónico no griego, preferimos sustituir este nombre por el de Demiurgo) :
.
A)- Fragmentos del Timaios, que preceden (o suceden) a la descripción de la temperación musical:.
- TIMEOS (31): "el Demiurgo (dios) comenzó a formar el cuerpo del universo, lo hizo de fuego y tierra. Pero no es posible que dos elementos solos se unan sin un tercero, pues es preciso que haya en medio de los dos una atadura que los una. La atadura mas perfecta es la que consigue que ella misma, o lo unido, se conviertan en una sola cosa" ..
Hace aquí claramente referencia a la idea de creación del Cosmos comparándolo con el de la concepción de un hijo (entre el hombre y la mujer) y por la cual, padre y madre se hacen "uno" -o "familia"-. De este concepto, como veremos mas tarde, pasa al la teoría del número de carácter pitagórico en la que del 1+2 nace el 3. Podremos apreciar que todo este texto es de origen y gran influencia pitagórica, aunque en ningún momento se cita al sabio de Samos, ni a su Escuela (pese a que Platón como veremos, entra en contacto con los pitagóricos en su viaje al sur de Italia). Por lo demás y a título de crítica personal, parece que en estos fragmentos, Platón deseara realizar algo similar a o que se cuenta hacía Ramón Gómez de la Serna, antes editar un artículo -o dar a conocer un discurso importante-. Literato novecentista español, del que narran que previamente a leer o a publicar en ambientes de prestigio, leía lo escrito a su "ama de llaves". Aquella "santa" que le cocinaba, limpiaba la casa y disponía en condiciones la ropa al escritor; parece que escuchaba con gran atención y esmero las palabras del "ilustre Gómez de la Serna". Quien tras haber leido plenamente el texto preguntaba a la buena mujer qué partes le gustaban más y qué había entendido como mejor. A lo que ella le respondía explicando las ideas que había comprendido y las que le parecían interesantes. Poco después y tras marcharse de la habitación el "ama de llaves", parece ser que "Ramón" profería las siguientes palabras con tono adusto: -"Esto que se entiende, hay que oscurecerlo; pero mucho... . Que ya sabes que en la vida todo lo que se comprende, no merece la pena"-.  (trás este terrible "lapsus" sigamos con el Timaios)
.
- TIMEOS (32): "Siempre que el término medio de tres números cualesquiera, enteros o cuadrados, haga que el primero se relacione con él mismo y con el último, y a su vez que el último se relacione con el término medio, y éste con el primero, siendo entonces el primero y último el término medio, y el último y el primero, por su parte, término medio, sucederá entonces, que necesariamente todos serán lo mismo, y siendo lo mismo entre sí, todos serán una sola cosa". 
.
Este fragmento que se pudiera intepretar como un texto ininteligible -en alguna medida-; consideramos que nos habla del (1, 2, 3...). Serie la que de que el 2 tiene igual distancia, intervalo o proporción hasta el 1 que hasta el 3. A su vez, que la distancia del 3 al 2, es la misma que la del 2 al 1; por lo que todos se relacionan de igual forma. Lo que indica que los tres números son uno; ya que en el 3, se contendrán los otros dos. Todo ello va dirigido sobre la teoría del número e Pitágoras, en la que hemos dicho que del simple "1" nacería el infinito. Algo que se explica porque en sí mismo, las cifras se generan a en serie y unas a otras en la forma ya descrita y por la cual:
.
(1+1) = 2 // (1+2) = 3 // (1+3) = 4 = (2+2) // (1+4) = 5 = (3+2) ......
.
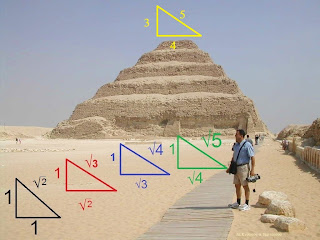
Desde estos conceptos y números, ya en anteriores entradas habríamos obtenido los dos grandes triángulos: Primero, el que hemos denominado "anatemático" (a=1, b=1, c=Ѵ2 ). Después el primer irregular (a=1, b=2, C= Ѵ5); y finalmente el "triángulo perfecto" (a=3, b=4, c=5).
-Todos los que en la imagen siguiente observamos y de los que "descienden" las grandes cifras como "fi" {Ѵ5+1) : 2} y "pi" (perímetro/diámetro).
- La cifra "pi" antiguamente seguramente se creyó procedía de una fórmula relacionada con la raiz cuadrada de dos y del tres; tal como vemos abajo. Algo que se hace inevitable al concebir (fue el modo común de calcular "pi" que usaban los egipcios).
.
BAJO ESTAS LÍNEAS: Hemos trazado algunos cálculos sobre el perfil de la "supuesta" hija de Akhenaton -Amenophis IV- (hacia el 1351-1334 a.C.); una talla en propiedad del Walters Art Museum, of Baltimore -Estados Unidos- (al que agradecemos nos permita divulgar la imagen con este fin). En los dibujos escritos podemos ver la simplicidad para hallar "pi" (o la raiz de dos) simplemente haciendo unos trazos sobre la arena -con palos y cuerdas-, para medir posteriormente las distancias en las figuras. En ellos hemos incluido el "pi" egipcio, que en las mediciones de sus edificios vemos que es evidentemente  . Igualmente la "raiz cuadrada" de dos, se pudo concebir como nacida de este "pi" o relacionada con él, siendo un cálculo muy aproximado de ella: (½ ) : (10/9) = Ѵ2.

Por su parte, el hallazgo de que "Pi" en Egipto se escribiera 22/7 es un hecho que ya mencionaba Peter Tomkins en los años ochenta; algo que se demuestra incluso en la Gran Pirámide, cuya base dividida por la altura es 1/2 de =11/7 Todo ello me llevó a concluir en ese tiempo que esta matemática se pudo hacer de manera fáctica y pintando sobre la arena las figuras. De tal manera, si trazamos un círculo pinchando un palitroque en el centro y girando sobre aquel con una cuerda atada a su extremo (que tenga otra estaca y vaya dibujando la circunferencia). Bastará con dividir el diámetro del redondel pintado, por la dos veces la cuerdecita central (que es El Radio); lo que nos llevará a una aproximación de "pi" muy cercana (mayor, cuanto más grande sea esta circunferencia que hagamos sobre la arena).
.
Tras obtener esa división (Radio : Diámetro), y concluir que "pi" es 11/7, veremos algo tan sencillo como que si dividimos aquel por 10/9 nos saldrá una cifra muy cercana a la "raiz de dos",. Es decir, que (11/7) : (10/9) es más o menos igual a Ѵ2 .
Todo lo que expresamos como (1/2 de ) : (10/9) ≈ Ѵ2 .

.

.
.
La serie por la que irían encontrando el resultado expresado que relaciona "pi" con "raiz de dos" partiría de que (22/7) : [2 + (2/9)] ≈ Ѵ2 .
.
O lo que es lo mismo: 3,142857... : (20/9) = 1,414285714... (una cifra que viene a ser casi igual a la verdadera Ѵ2 = 1,4141213562...)
.
De todo lo que se llegaría a deducir que la "raiz cuadrada de dos" se entendía unida a el "pi" de 22/7; y esta como 1,414285714... ≈ Ѵ2 .
Es decir que {½ : (10/9)} = Ѵ2 ; o bien :20/9 = Ѵ2

.
Considerando esa raiz de dos una Cifra que se podía escribir en la forma 198/140 = 1,414285714... y cuyo cuadrado exacto es 2,000204082... lo que le aproxima mucho a 2. Es decir:
.
(198/140)^{2 
= 2,000204082... ≈ 2}
y por su parte
(198/140)2 = [(22/7) : (20/9)]2
.
de lo que se podía dedir que más o menos, 
2 es igual al cuadrado de "pi" dividido por 20/9
(+  -) 2 ≈ ( : 20/9)2
.
Siendo así y partiendo de que a través de medir los catetos e hipotenusas de los triángulos, tanto como la relación entre el diámetro y el perímetro se pude llegar a la conclusión o aproximación que vemos los edificios egipcios manifiestan por la que:
.
Ѵ2 = 99/70
. = 22/7

.
Todo lo que relacionaría del mismo modo al número siete con ambas cifras. Ya que se la raiz de dos podía expresar en séptimos, con la forma 99/70 (aproximación muy carcana a Ѵ2 ) o bien 22/7 (como la aproximación muy utilizada en la antigüedad como ). Existiendo pues una relación plena entre "pi" y la "raiz de dos" que es simplemente 0,45; habida cuenta que 22/7 · 0,45 = 99/70.
.
Siendo así, veríamos que escrito a modo antiguo 100/45 es la relación entre "pi" y la "raiz de 2". Ya que (100/45) · (99/70) = 22/7
O lo que sería lo mismo: Ѵ2 · (100/45) = 
.
Regresando al texto platónico que analizábamos y que era el fragmento TIMEOS (31): "el Demiurgo (dios) comenzó a formar el cuerpo del universo, lo hizo de fuego y tierra. Pero no es posible que dos elementos solos se unan sin un tercero, pues es preciso que haya en medio de los dos una atadura que los una. La atadura mas perfecta es la que consigue que ella misma, o lo unido, se conviertan en una sola cosa" . Diremos nuevamente, que para entender lo que expresa, recordamos el ejemplo de la creación del hijo por padre y madre. Aunque la exposición que nos plantea Platón en "Timeos-31", contiene un planteamiento muy similar al que unos siglos mas tarde daría la fórmula de expresar las relaciones de "FI" o la Sección Aurea (puramente "euclidiana"). De este modo, Euclides en "Los Elementos" nos habla de que la Proporción Aurea es cuando: En una porción de tamaño "C", con una división "B" en su centro, y un punto "A" de inicio, se cumple la siguiente relación. Cuando la distancia de A a C, dividida entre la que hay entre B a C; es igual a la longitud de B a C,dividida por la que hay de A a B. Es decir: AC / BC = BC / AB
.
Pese a ello, la concepción de "fi" por los egipcios y la que quizás aún se tuvo en epocas de Platón, pareció ser otra y muy relacionada con "pi" (tanto como con la raiz cuadrada de dos). Acerca de número áureo en las construcciones de los sacerdotes del Nilo, ya nos advierte Tomkins que se encontraba en la Gran Pirámide y en la fórmula de dividir entre la "catenaria" y su base. Denomino "catenaria" a lo que vulgarmente en construcción se denomina "sección de un tejado"; pero que en matemática se ha de decir "apotema" o "hipotenusa" -que es el vértice que va desde la cúspide a la base, recorriendo por su centro la "cara" de la pirámide-. Pese a ello, si la recordamos como "catenaria" rsulta fácil comprender las siglas de los triángulos y pirámides; ya que (a)=Altura; (b)=Base y (c)=Catenaria.
.
Pero regresando a "fi" entre los egipcios, deduzco como cierto, sabiedo que la altura de la Pirámide de Kefrén era de unos 147 metros y su base de unos 231 metros. Que si trazamos un triángulo dentro de aquella tomando como "cateto (a)" (Altura) y "cateto (b)" (1/2 de la Base); el resultado es que la "catenaria (c), sería de unos 186,94... metros. Una hipotenusa (c) -o apotema-, que dividida por el "cateto b" resulta una cifra muy cercana a "fi". Así lo advirtió ya Tomkins (tal como decimos) aunque en los años ochenta no se "profundizó en las consecuencias" mateáticas que este hecho tiene. "Consecuencias" entre las que se halla el hecho de que "pi" y "fi" desciendan de unos mismos números. Es decir que si:
.
Ѵ(a2+b2) = c
.y a su vez; c / b = 
Sucediendo esto cuando b / a =  / 4
Todo ello considerando a "pi" como 2 ≈ ( : 20/9)2
o lo que es lo mismo  = 22/7.
.
Se deduce que los egipicios verían la relación existente entre "pi" y "fi" del siguiente modo que recogemos en imagen (tal como expresa y se deduce de la Gran Pirámide). Siendo la cifra  que resulta de dividir la base por la catenaria: 1,6180339887 . Un número cuya aproximación al "fi" matemático (1,61859034678...) es verdaderamente impresionante.
.

. 
SOBRE ESTAS LÍNEAS: De nuevo hemos trazado algunos dibujos sobre el perfil de la hija de Akhenaton -Amenophis IV- (hacia el 1351-1334 a.C.); una talla en propiedad del Walters Art Museum, of Baltimore -Estados Unidos- (al que agradecemos nos permita divulgar la imagen con este fin). En las figuras se observa la relación de altura y base en La Gran Pirámide, que es 4 . O lo que es lo mismo: (2Bases : Altura) =  = 22/7 . Por su parte, si dividimos el "apotema" (hipotenusa o catenaria) por la base (b) veremos que el resultado es casi "Fi". Un número áureo egipcio que coincide practicamente con el que más tarde la matemática euclidiana explica.
.
Siendo así nos queda el problema de saber si el origen de este número fue arquitectónico y perteneció a las "artes espaciales" o si muy por el contrario la idea de "fi", nació desde la música. Un hecho que parece más cierto al observar que el mismo Platón nos habla de aquella proporción (de manera muy semejante a la que siglos después utiliza Euclides), nada más dar comienzo su tratado sobre el modo de lograr la afinación. Ello hace deducir que el "número áureo" procede fundamentalmente desde valores ligados a los temperamentos y que tras su aplicación a la música, pudo ser deducido como una fórmula armónica y de estética en las artes plásticas. Algo que parece más que lógico, pues de lo contrario y sin su justificación como el origen del sistema para hallar las notas musicales, es muy difícil deducir esta cifra de un modo aleatorio y como imprescindible en la estética universal. Más claro: Si proponemos una sección como perfecta, quizás no podemos demostrar físicamente que afecta a la armonía. Pero si la necesidad de esa proporción la relacionamos con el principio de afinación y creación de las notas musicales, parecerá cierto que es la base de toda la armonía.
.
Por cuanto decimos, siendo el origen de la división de la "octava" musical y de sus doce notas, esta fórmula. Se hace evidente que "el número de oro" afecta al equilibrio armónico. Un hecho que muchos definen como mágico, pero que en verdad a de ser visto como místico; ya que hay belleza en todo objeto o sonido, siempre que la proporción entre A B y C sea la descrita antes:
.
Cuando la distancia de A hasta C, dividida entre la que hay entre B hasta C; es igual a la longitud de B hasta C,dividida por la que hay de A hasta B. Es decir: AC / BC = BC / AB).
De todo ello y de "algo más" seguiremos hablando en las siguientes entradas.

EL ANATEMA PITÁGORICO: Nota explicativa a la anterior entrada

Este artículo es una ampliación a la anterior entrada -VER: http://decnossosatartessos.blogspot.com.es/2013/08/un-modo-de-comprender-f-la-seccion.html -
.

.

.
SOBRE ESTAS LÍNEAS: De nuevo una fotografía del autor de estos artículos, junto a la pirámide de Shaqqara, tal como la subíamos en anterior entrada. He pintado sobre la imagen los ejemplos de triangulación que exponíamos como nuestra idea para hallar las raices cuadradas en la Antigüedad más remota. Un método fáctico, basado en dibujar escalenos o equiláteros en la arena (por medio de palos y cuerdas), en la forma que a continuación describo. Acerca del anatema pitagórico tal como lo veo (que me comenta un lector "mal explicado" -ya que habíamos incluido una imagen de una triángulo con valor "1", "1" e hipotenusa ¿2?-) ; a continuación lo analizamos de nuevo para que todos los que nos siguen puedan entenderlo facilmente y sin errores. Pese a ello y como adelanto les propongo que reflexionen sobre estos triángulos dibujados en la parte superior de la imagen. Ya que el anatema se produce habida cuenta que: 1 = Ѵ1 = 1^{2 .
Lo que produce el "desfase" en la representación triangular de la raiz cuadrada de "2". Tanto más cuando no se puede aplicar geométricamente el teorema pitagórico con catetos con valor menor a 1.}.
.
MÉTODO FÁCTICO EGIPCIO PITAGÓRICO QUE HEMOS PENSADO PARA OPERAR CON RAICES, EN BASE A TRIÁNGULOS Y EL PROBLEMA DEL ANATEMA DE PITÁGORAS:
 a)-. MODO DE REALIZARLO:
-
Bastará partir del primer triángulo, que será : cateto (a)=1 ; cateto (b)=1; cuya hipotenusa es Ѵ2 (hallando así el valor de esta raiz cuadrada del 2). Para ello, trazaremos en la arena el cuadrado (o triángulo) lo más perfectamente que podamos y con valor -por ejemplo- de 1 metro en cada lado. Tras lo que midiendo perfectamente su raiz del cuadrado (la hipotenusa) veremos que equivale a la de Ѵ2 = 1,414213562. VER EN IMAGEN INFERIOR EL TRIÁNGULO ROJO SOBRE EL CIELO (a la izquierda y marcado con una a): Su "raiz del cuadrado" 1 x 1 es Ѵ2.
.
Aunque ello plantea ya el problema de lo que consideramos era el famoso "dogma" que se interpretó como que Pitágoras negaba la raiz del 2. Porque por debajo del 1 no se puede representar geometricamente su teorema, dado que 12 y Ѵ1 es lo mismo que 1. El problema se acrecienta cuando se baja del valor 1, dado que la raiz cuadrada de 1/2 es superior a 0,5 (Ѵ1/2 = 0,707106...). De lo que ya el triángulo "1", "1" , plantea la duda de si el resultado es en verdad y su hipotenusa equivale a Ѵ2 (tal como el filosofo explicaba).
.
b)-. EXPLICACIÓN DEL ANATEMA:
.
Si queremos hallar las raices de 1/2 (0,5), y representarlas en geometría; teoricamente bastará con obtenerlas realizando un triángulo cuya hipotenusa es "1" ; dibujando dos catetos iguales bajo este -aprovechando el lado del anterior, para que este se convierta en la raiz del nuevo cuadrado-. De tal manera y midiendo minuciosamente los lados de este, sabremos que los catetos idénticos cuya hipotenusa es "1", serán la raiz cuadrada de 1/2 = Ѵ0,5. VER IMAGEN BAJO ESTAS LÍNEAS EN NEGRO, LA SEGUNDA Y MARCADA CON b).
.
Pese a ello, esto no es tan sencillo de comprobar ni de ver como cierto, ya que la raiz del cuadrado de 1/2 es superior a 0,5. Siendo así, que para una hipotenusa de 1 se precisan dos catetos de 0,70710681 = Ѵ0,5 .
.
Por lo que si (Ѵ1/2 = 0,707106...) y si (0,707106... x 2 = Ѵ2) su hipotenusa sería ѴѴ2, es decir 4Ѵ2 raiz cubica de 2; o lo que es lo mismo 21/4
.
Con esta explicación creemos que se entiende "el dogma" de Pitáguras, que incluso dudaba de que la hipotenusa del triángulo "1", "1" fuera realmente Ѵ2 .
.
c) LA TRIANGULACIÓN:

.
1º POR RAIZ DEL CUADRADO:
En el lado superior derecho, sobre la zona de cielo y marcado como (c), podemos ver el primer desarrollo de estos triángulos, de los que se forman gradualmente con los siguientes valores:

Primero y en amarillo: "1" - "1" - raiz del cuadrado = Ѵ2

Segundo y en naranja: "Ѵ2" - "Ѵ2" - raiz del cuadrado = 2

Tercero y en color rojo: "2" - "2" - raiz del cuadrado = Ѵ8

Cuarto y en negro: "Ѵ8" - "Ѵ8" - raiz del cuadrado = 4 (marcada en morado).

.
2º POR TRIÁNGULOS:
Es este un sistema sencillo de hallar raices cuadradas de números enteros dibujando en la arena triángulos. El sisteme que se nos ocurre es tan simple como el trazado de triángulos consecutivos, que comienza en el "1", "1", "Ѵ2" y que como hemos realizado en el esquema termina en "1", "Ѵ8" , "Ѵ9"

Primero, amarillo: Cateto (a) 1; (b) 1, Hipotenusa Ѵ2

Segundo, naranja: (a) 1 , (b) Ѵ2 , Hipotenusa Ѵ3

Tercero, rojo: (a) 1 , (b) Ѵ3 , Hipotenusa Ѵ4

Cuarto, negro: (a) 1 , (b) Ѵ4 , Hipotenusa Ѵ5

Quinto, morado: (a) 1 , (b) Ѵ5 , Hipotenusa Ѵ6

Sexto: azul: (a) 1 , (b) Ѵ6 , Hipotenusa Ѵ7

Séptimo, verde: (a) 1 , (b) Ѵ7 , Hipotenusa Ѵ8

Octavo, marrón: (a) 1 , (b) Ѵ8 , Hipotenusa Ѵ9

Así, sucesivamente hasta hallar las raices cuadradas que se deseen.

.

Un modo de comprender "la sección áurea"; como "número perfecto" nacido de la triangulación sagrada entre las civilizaciones más antiguas

CAPÍTULO 2 de: Hipótesis arqueológica sobre las primeras temperaciónes y escalas musicales.
.
BAJO ESTAS LÍNEAS: Sobre una fotografía de la clave central de la Catedral Vieja de Salamanca, hemos dibujado el cuadro que denominamos El Mundo Objetivo y Subjetivo, aplicado a las artes, a las ciencias y a las humanidades. Un esquema que ya presenté como tesis hace unos treinta años; haciendo de este un principio de análisis sobre el cual poder comprender por qué unas disciplinas son mediatas (lejanas) a otras y algunas están unidas inmediatamente. De tal modo y por muy diferentes que nos resulten las humanidades de la ciencia o del arte, se sitúan a medio camino y entre ambas disciplinas. Por su parte, la ciencia pura y las artes, se hallan en polos opuestos; tal como se encuentran las humanidades que hemos llamado sociales (economía, polítología, Derecho...) de las intelectuales (filología, Historia etc).
.
En este esquema que hemos trazado sobre la foto de la clave, podremos ver que hay un mundo SUBJETIVO SUBJETIVO -marcado como (A)- y que se corresponde al de las artes; y que como todos entendemos, son puramente subjetivas. A su lado se sitúa el terreno de lo SUBJETIVO OBJETIVO (B), que comprende humanidades como la sociología, el Derecho, o la economía -a las que llamaremos HUMANIDADES SOCIALES-. Ello porque para el análisis de estas ciencias se ha de partir desde hechos subjetivos (comunes a todos), necesitando más tarde aplicar procedimientos objetivos (como la matemática, la estadística o la criminología). Siendo el fundamento de estas disciplinas partir desde hechos subjetivos para llegar a unas conclusiones objetivas y ecuánimes. De ello considero lao que denomino "humanidades sociales", como SUBJETIVAS OBJETIVAS.
.
Bajo las anteriores podremos hallar el mundo de lo OBJETIVO OBJETIVO (C); que se correspondería con la ciencia pura (como la matemática). A su lado, finalmente veremos el OBJETIVO SUBJETIVO (D); que catalogamos de HUMANIDADES INTELECTUALES (filología, Historia, etc). Ello porque estas disciplinas parten desde unos hechos objetivos (históricos, lingüísticos etc), para llegar a conclusiones puramente subjetivas (o personales de cada historiador, literato y estudioso).
.
Siendo así y frente a este esquema tendremos las bases para comprender por qué se produce la "trascendencia" o la sublimación (que llega al misticismo). Un hecho que se lleva a cabo cada vez que una disciplina o arte logra pasar hasta su lado mediato. Por ejemplo, cuando la matemática y la física llegan a unirse con la música, con la pintura y otras artes; al igual que se sucede la "trascendencia" en el momento en que el arte tiene un enorme contenido de conocimientos científicos puros, logrando a que su belleza se transforme en ciencia. Algo que sucede -como siempre decimos- y puede observarse perfectamente en las construcciones de las catedrales, en la música de Bach, o en la obra de pintores como Leonardo da Vinci (cuyos principios artísticos se relacionan con teoremas matemáticos). De un igual modo, las teorías científicas de Kepler o de Newton tienen tal belleza y sublimación, que son una obra de arte. Siendo así, cuando el arte está pleno de ciencia -o cuando la ciencia se convierte en arte-, ambos habrán transcendido a un plano sobrehumano o sobrenatural. Es lo que comunmente denominamos "elevación" o mística.
.
En el caso de las otras dos clasificaciones: Del mundo SUBJETIVO OBJETIVO (B), frente a lo OBJETIVO SUBJETIVO (D). La tarscedencia se produce en el momento en que alguna disciplina pasa a su estado "mediato". Es decir, que (B) se acerque a (D) o viceversa; sin poder distinguirlas. En ese instante se produce la filosofía (del Derecho, de la econimía, de la política, de la Historia o de la lingüistica). Un pensamiento filosífico social en el caso de que (B) se confunda con (D); o bien filosofía puramente "intelectual" en el contrario -cuando (D) se acerca a (B)-. Ello porque al llegar el pensador hasta un mundo "mediato" (ajeno), las hipótesis y las formas de trabajo se convierten en las inversas. Para que lo entendamos, pensemos en el jurista o el economista, que tras hacer un análisis de los subjetivo y obtener unas conclusiones objetivas; se plantea de nuevo trabajar las mismas ideas del modo contrario Todo lo que le llevará a crear un sistema filosófico en el cual considerará que su conclusión -objetiva- es fruto de un estado constante de subjetividad en el Hombre. Por cuanto en la economía se analizarán los factores culturales, los gustos sociales, o los modos de vivir (no la estadística ni la lógica); al igual que en el Derecho se estudiará la moral o las conductas (subjetivamente hablando) y no el código práctico que lleve a aplicar lo más útil en cada caso.
.
Conociendo lo que consideramos una explicación teórica de la trascendencia, continuaremos analizando la música y la matemática, como un medio de sublimar la espiritualidad.
.

.
A) LA TRASCENDENCIA MÍSTICA O LA SUBLIMACIÓN "ELEVADA"; SITUACIÓN EN QUE SE ORIGINA:
. 
Hasta ahora habíamos hablado de los métodos de afinación como una técnica o concepto que partía desde conocimientos científicos, técnicas que llegaban a extrapolarse hasta unas ideas filosóficas que la unieron con las distancias y fuerzas del Cosmos. Teoría que por muy absurda que pueda parecernos, fue el comienzo de las Leyes de Kepler, tanto como la clave para que Newton resolviera su ecuación sobre la Fuerza de la Gravitación. Pese a ello, los "orígenes místicos" de las escalas musicales son milenarios, debiendo remontarnos al tiempo de Las Pirámides; momento en el cual debieron nacer estas ideas que equiparaban las fuerzas y ritmos del Cosmos, con los de la música. Un pensamiento de gran belleza y cuyos conceptos puramente filosóficos llegaron a poder demostrarse miles de años tras ser creadas y escritas.
.
Por cuanto puede dedcirse históricamente, podemos afirmar que durante la Edad del Bronce hubieron de generar estos principios que concedían un carácter sagrado a las notas y a su afinación. Un "dogma místico" que heredaron los filósofos de la Primera Edad del Hierro, quienes cosideraban las artes de "temperar" -templar- los instrumentos, plenamente relacionadas con la Creación del Universo. Es decir, que se concebía el nacimiento de Espacio en virtud de unas medidas y divisiones iguales a los intervalos de las notas, en la escala musical perfecta. Todo lo que concedía un espíritu místico a la música, que incluso la unía e igualaba al origen del Espacio y del Tiempo. Ello porque pese a que Lessing catalogara a este arte de la acústica como puramente temporal, los antiguos lo concebían medido por distancias y pesos (tal como los astros gravitan). Es decir que las notas y sus intervalos se regulaban por longitud y tensión de cuerdas -en los cordófonos-, el tamaño de las "cañas" -en los instrumentos de viento-, o el peso y el volumen -en los de percusión-. Siendo así, el espacio regulaba una perfecta armonía y el tiempo un ritmo exacto. Un hecho que unía a la música con el Cosmos, igualmente medido por distancias y por sucesiones de periodos siderales, todo ello "atado" por una fuerza -gravitatoria- que tensaba y unía los planetas, de un mismo modo que el diapasón (o el clavijero) sujeta y regula las cuerdas.
.
Una idea de Armonía Universal de la que surge la Musica de las Esferas, comunmente considerada platónica (o pitagórica), al haber sido divulgado y enseñado ese "dogma del Temperamento" por aquellos dos filósofos. Pese a ello, esta teoría que une los planetas -sus distancias y ciclos-, con la acústica y el "número perfecto"; tiene sus orígenes en las religiones más antiguas de Mesopotamia y de Egipto. Basándose en unas creencias nacidas al sublimar la matemática, la astronomía y las artes, uniéndolas a la espiritualidad -seguramente interpretando la capacidad para comprenderlas como un "don" divino-. Método por el cual lograban tal transcendencia al unir el sentimiento de la belleza artística con las teorías científicas; que trasladan el mundo puramente subjetivo (las artes) al pensamiento más objetivo (como la física o la matemática). Este avance por el cual se consigue unir la ciencia pura, a las disciplinas artísticas y a las humanidades más profundas (la filosofía), es un salto trascendente desde el mundo "objetivo" hasta lo más "subjetivo" del hombre. Consiguiendo a través de ello generar en nuestro interior un estado de elevación o deificación inigualable. Siendo a mi juicio este el motivo por el cual las artes que logran superar el mundo subjetivo y acercarse al terreno de las ciencias (de lo puramente objetivo), logran transmitirnos un estado y unas sensaciones místicas -o de elevación sublime (como sucede por ejemplo con la música de J.S. Bach, o con la pintura de Piero de la Francesca)-.
.
BAJO ESTAS LÍNEAS: Algunos de los primeros triángulos en el plano, dibujados por mí sobre una foto tomada en la pirámide de Saqqara -recogemos esta imagen recordando la belleza de Egipto, ante los momentos de crisis que sufre este país milenario en nuestros días; deseando que sus problemas se solucionen pronto, de forma pacífica y estable-. En la ella vemos el monumento escalonado creado por el "gran arquitecto" y visir (schaty divino) Imhotep, a comienzos del III milenio a.C.. Siglos en los que ya se establecen las medidas ("el Maat" de Egipto) como "número y equilibrio perfectos", nacidos desde la armonía del Universo. 
. 
En la imagen, en primer plano y en azul (sobre la arena) TRIÁNGULO INICIAL de "1" y "1", cuya hipotenusa es =  √2. A la izquierda y sobre el cielo (en amarillo), el SEGUNDO TRIÁNGULO, con "1" y "2", cuya hipotenusa es =  √5. Al lado opuesto (en rojo) el primer triángulo de gran imperfección que es de "2", "3"; ya que su hipotenusa = √13. Una raiz de trece que carece de sentido estético en la progresión que estas figuras, ya que por ejemplo el "1" y "3", tendría una hipotenusa √10 ; longitud y raiz que de algún modo debió ser considerada bella (al menos entre los egipcios que utilizaban base decimal). Por su parte y en la zona central -tal como explicaremos-, hemos trazado una fórmula para poder hallar todas las raices cuadradas, valíendose simplemente de triángulos dibujados en la arena.
.

.
A) EL ANATEMA DE LA RAIZ CUADRADA DE "2" Y EL PROBLEMA PITAGÓRICO:
.
Uno de los temas más "peliagudos", cuando tratamos sobre Pitágoras y sus discípulos es el famoso "dogma de la raiz cuadrada del dos"; sobre el que algunos autores mantienen que "el maestro" afirmaba, no existía. De un modo tal que las leyendas llegan a narrarnos como uno de sus discípulos logró descifrar el valor de √2= 1,4142135... ; trás lo que el resto de compañeros de "secta" ordenaron matarlo (o expulsarlo, por ir contra los principios del pitagorismo). Algunas fuentes hablan de que aquel descubridor del anatema , fue el grán arpista y filósofo Terpandro de Lesbos. Pese a lo que en verdad, este músico y teórico de la armonía fue juzgado y castigado por crear una nueva afinación y generar dos notas distintas (en la escala pitagórica). Por lo demás, mucho nos extraña a quienes hemos estudiado esta filosofia, que los seguidores de Pitágoras proclamasen la inexistencia de la raiz cuadrada del 2; ya que ella es el fruto del primer triángulo. Es decir, que cuando un "cateto" mide "1" y el otro es también igual a "1", su hipotenusa será = √2.

.
Existen teorías que afirman también la imposibilidad de cálculo en la Antigüedad de raices cuadradas como la del "2", al carecer de cifras ni de escritura en fraccoiones. Pese a ello, hemos pensado durante algún tiempo cómo pudieron calcular la  ; deduciendo que para hallarla nos bastará con trazar sobre la arena un triángulo -o un cuadrado- de un metro de largo en cada cateto (procurando que sean exactamente iguales). Tras ello, si medimos bien la longitud de su "raiz del cuadrado central" (la hipotenusa), hallaremos pronto el valor cercano de  √2, como 1,4142135... . Un hecho que nos traslada a las matemáticas fácticas, que en mi opinión y teoría fueron las que estudiaron, "vivieron" y calcularon en el Egipto antiguo (incluso hasta en Grecia y Roma). Un método matemático donde el trabajo con cuerdas, con cálculos (piedrecitas) y a través de dibujos en la arena, debió ser la fórmula para encontrar ciertas operaciones (que más tarde se comprobaban por teoremas).
.
Además, la justificación matemática de aquellas no era tan importante como su utilidad; pues tan solo deseaban poder trabajar con los resultados así obtenidos. Tanto, que una aproximación bastaba para tener la cifra necesaria ( etc). Siendo para ello suficiente, trazar circunferencias, triángulos o cuadrados, a la perfección; y después medirlos minuciosamente en sus distancias y proporciones (con cuerdas). Resolviendo así -por ejemplo- la trigonometría esférica; que permite recoger conocimientos utísimos para guiarse en el desierto, o calcular la hora y fecha (pudiendo viajar bajo la prospección de longitud y latitud, conociendo así donde nos encontramos en cada momento de la singladura).
.
De tal manera, pensando en esta primera conclusión que exponemos; nos será muy fácil comprender qué significaba "la cuerda" para los sacerdotes egipcios (tanto como para los agrimensores griegos o romanos). Quienes debían valerse de sogas no solo para el estudio de la matemática, sino también como el mejor medio para medir las propiedades, las distancias en los caminos y para distribuir las parcelas. Un trabajo en el cual era imprescindible manejar la triangulación, habida cuenta que el cuadrado -o el rectángulo- se deforman facilmente. Aunque el triángulo no pierde tan rápidamente su perfección, ya que valiéndose de una simple escuadra puede comprobarse si su vértice está o no a 90º (delatando su estado defectuoso con bastante exactitud). A ello seguramente se debe la importancia del triángulo en Egipto, al igual que la concedían a "la cuerda". Esta última tristemente desconocida, aunque una de la ceremonias más importantes fuera la de extensión de cuerda. Rito con el que comenzaba toda obra de construcción (en especial si era sagrada), y con la que iniciaban o inaguraban los templos, al igual que algunas fiestas. Siendo la cuerda el utensilio más útil para el agrimensor, tanto como para el matemático; ya que valiéndose de aquellas y dibujando sobre la arena, podría calcular difíciles ecuaciones, raices, y hasta manejar la trigonometría esférica (o circular, realizando complejos algoritmos). Todo ello valiéndose tan solo de unas sogas, unos palos (o un bastón) y de un sistema de medidas perfectamente delimitado.
.
BAJO ESTAS LÍNEAS: Fresco egipcio perteneciente a una tumba de Tébas (Valle de los Reyes) fechada en el Reino Nuevo (XVIII dinastía) -agradecemos a la institución propietaria, nos permita divulgar la imagen-. En la foto observamos unos funcionarios (¿sacerdotales?) que trabajan con su cuerda, midiendo el campo de cereal, para calcular la extensión y producción -con el fin de cobrar impuestos y generar un reparto ecuánime y justo de los recursos-. Tras el personaje que porta la soga se observa un segundo individuo que lleva un bastón; mientras frente ellos (a nuestra derecha y en lugar que apenas se ve) existe un tercer personaje que sujeta algo que bien pudiera ser una escuadra -o un método de calcular los grados de la soga extendida-.
.
Evidentemente, la imagen nos habla de personas muy preparadas para la agrimensura, que se esmeraban en calcular perfectamente el reparto de tierras y la producción de cereal, con el fin de cumplir su cometido de un control justo sobre la Sociedad. Por lo demás se sabe que tales cuerdas eran preparadas durante meses en los recintos sagrados, donde igualmente se marcaban sus medidas para evitar fraudes. Las extendían y "curaban" al sol (y con agua) por un tiempo largo, tras lo que untaban con grasas y resinas estas sogas, con el fin de que no sufrieran deformaciones y midieran perfectamente cada caso. Portando marcas absolutamente delimitadas, que tras la supervisión del templo se consideraban exactamente calculadas; eran tan útiles como puede resultar en nuestra civilización la cinta métrica.
.

.
Pero siguiendo con la teoría de los triángulos, y el problema del "2", tan solo concebimos que Pitágoras afirmase al inexistencia de la raiz de este número, refiriéndose a una extraña realidad, como es el hecho de que si tomamos varios triángulos equiláteros con el vértice a 90º, sus catetos siempre serán la raiz cuadrada de la hipotenusa dividida entre "2". Es decir, que si la hipotenusa es 4, ambos catetos serán Ѵ4/2; si la hipotenusa es 3, los dos catetos serán Ѵ3/2 y así sucesivamente. Aunque existe un caso, que es el "2", en el que vemos algo tan extraño como que Ѵ2/2 = Ѵ1 = 1. Es decir que realmente el triángulo cuya hipotenusa es "2", tiene dos catetos que carecen de raiz cuadrada, ya que ella es igual a "1". Habiendo sido muy probablemente este al anatema pitagórico, habida cuenta que es el "1" el que de algún modo no tiene raiz cuadrada. Al consistir en un número tan extraño que su elevado o raiz cuadrada es igual a sí mismo: 1^{1 = Ѵ1 = 1·1 = 1 .}
.
BAJO ESTAS LÍNEAS: El autor de estos artículos junto a la Pirámide de Saqqara. Al lado he ido dibujando la sencilla forma del triángulo en la que cuando una hipotenusa es "x" y los dos catetos son iguales; ambos son =Ѵx/2. Este quizás fue el problema con el que se encuentra el pitagorismo al observar que en con hipotenusa "2", y catetos idénticos, estos equivalen a "1"; es decir, realmente a 2/2; y no tanto a Ѵ2/2 (como debiera ser). Considero por ello que quizás el "dogma pitagórico" acerca de la Ѵ2 debemos entenderlo así; al creer posiblemente los seguidores de Pitágoras, que en verdad el número que carece de raiz cuadrada es el "1" (cuya hipotenusa en el primer triángulo "1", "1" es = "2"; y de ello el anatema relativo a la raiz de este segundo número). 
.

.
Continuando con la matemática fáctica, si tomamos como el primer triángulo el antes estudiado ("1", "1", "2"); el siguiente en relación a un orden numérico, sería aquel cuyos catetos fueran "1" y "2". Un triángulo cuya hipotenusa -como vemos en la foto de abajo- es Ѵ5 = 2,2360679... . Siendo así, para calcular la raiz cuadrada de 5 en la antigüedad, vemos que bastaría con trazar sobre la arena un triángulo de estas medidas: "1" en el cateto (a), "2" en el (b); siendo (c)=Ѵ5 . Todo lo que se calcularía midiendo bien la hipotenusa, para cuyo conocimiento semi-perfecto quizás haría falta realizar figuras de enormes medidas; aunque -realmente- si deseamos comprobar su facilidad para hallarlo de este modo, bastará que pintemos sobre la arena de la playa un triángulo con un metro en su lado (a) y dos de largo en el (b); para luego medir con exactitud la hipotenusa, observando que (c) nos resultará un valor muy cercano a la verdadera Ѵ5 = 2,2360679... .
.

BAJO ESTAS LÍNEAS: De nuevo una foto de la Pirámide se Saqara, aunque ahora hemos dibujado sobre aquella un sistema para hallar cualquier raiz cuadrada de modo fáctico. Para lo que bastaría partir desde el primer triángulo ("1", "1", "Ѵ2" ) y seguir en un modo escalonado siempre que el cateto primero (a) fuera = "1" De tal modo con (a)=1; el cateto segundo (b) sería la hipotenusa del triángulo anterior. Ello así medido nos daría la razón continuada de las raices de Ѵ2; Ѵ3; Ѵ4; Ѵ5; Ѵ6; Ѵ7 y etc. En la foto podremos ver representado el método de ir dibujando en el suelo o sobre la arena estos triángulos sucesivos (que generarían una especie de "escalera" formada por triángulos consecutivos).
.
 
.
B) LA RAZÓN PRIMERA DE "FI" () Y DE LA AFINACIÓN PITAGÓRICA: 
. 
Trás observar la anterior relación de triángulos y su uso para hallar fácticamente las raices cuadradas, nos será fácil comprender que los egipcios y mesopotamios, pronto encontrarían el llamado "triángulo perfecto". Un escaleno que consistía en "3", "4", "5"; triángulo del que sabemos hubo de ser sagrado para los sacerdotes del faraón, por cuanto se repite en las formas arquitectónicas. Tanto que algunos autores (como Peter Tomkins) creyeron haberlo visto en las proporciones del pene del dios Minu. Un divo-faraón que representaba la fertilidad del Nilo y el poder fecundante de sus limos en la inundación. Todo lo que se simbolizaba en este dios al que se considera el recuerdo de una de las primeras dinastías reinantes y procedentes del Sur: Gentes que invadieron el delta -o llegaron a este- desde el Bajo Egipto y a comienzos de la Edad del Bronce. Una migración de pueblos camíticas, que debió de demostrar la mayor fertilidad y fortaleza de los africanos, frente a la debilidad y falta de masa corporal entre los más "blanquecinos" (al menos para soportar las temperaturas y trabajar en las condiciones que el Nilo y sus campos precisaban). Tanto fue así, que Minu (el divo de la fecundación) era representado como un hombre de raza negra, vestido de faraón y con flagelo; mientras su pene erecto, como símbolo de la fertilidad y la riqueza, dicen algunos que marcaba la perfección en la creación: El triángulo "3", "4", "5".
.

ABAJO: Relieve capilla blanca de Sestrosis I, en Karnak (XII dinastía) -agradecemos a la dirección del Templo de Karnak (en Luxor), nos permita divulgar esta imagen-. En este podemos observar al faraón divinizado Min (ó bien Minu); dios de la fertilidad, que presenta el pene en estado itifálico. Algunos autores consideran que las medidas existentes entre el final de glande y la altura de su ombligo, conforman comunmente en las estatuas de Minu la proporción del triángulo perfecto (3-4-5). Así lo afirmaba el ingenioso investigador sobre las pirámides, Peter Tompkins -a mediados de los años ochenta-; estudioso al que se debe uno de los más entretenidos libros acerca de las construcciones egipcias. 
.
. .
.
Pero continuando con la razón de "fi" -también llamada "La sección áurea"; e incluso la Divina Proporción, durante el Renacimiento-; diremos que su comienzo o sus orígenes se hallan en este triángulo perfecto. Debido a que la relación entre sus catetos y su hipotenusa son las siguientes:
.
- a:b = 3/4 = 0,75 ; cuyo inverso es 4/3 = b:a

- a:c= 3/5 = 0,60 ; cuyo inverso es 5/3 = c:a

- b:c = 4/5 = 0,80 ; cuyo inverso es 5/4 = c:b
.
Siguiendo con sus proporciones, uniendo los catetos y la hipotenusa estas son:
.
- (a+b):c = (3+4)/5 = 7/5 ; cuyo inverso es 5/7 = c:(a+b)

- (a+c):b = (3+5)/4 = 8/4 ; cuyo inverso es 4/8 = b:(a+c)

- (b+c):a = (4+5)/3 = 9/3 ; cuyo inverso es 3/9 = a:(b+c)
.
Consecuentemente las proporciones que nacen de dividir sus lados (solos o bien sumados) son: 3/4 (inverso 4/3); 3/5 (inverso 5/3); 4/5 (inverso 5/4); 7/5 (inverso 5/7); 8/4 (inverso 4/8); 9/3 (inverso es 3/9). Unas divisiones que marcan claramente los temperamentos pitagóricos, cuyos intervalos de afinación en la escala musical son exactamente esos: 3/4 ó 4/3 (a la que s denomina "cuarta"; 3/5 ó 5/3 (que combina "quinta" y "cuarta"); 4/5 ó 5/ (que es el intervalo de "quinta"); 7/5 ó 5/7 (en relación con armonía de "quinta"); 8/4 ó 4/8 (la octava o diapasón); 9/3 ó 3/9 (cuya proporción es 3 o 1/3, igualmente relacionado con la "cuarta" en la escala musical).
.
Siendo así ya podemos afirmar que el sistema pitagórico de afinación y sus intervalos, proceden de estas medidas que marca el triángulo perfecto (3,4,5). Aunque sabiendo que aquellas escalas de Pitágoras y sus discípulos también estaban fundamentadas en la razón de "fi", nos será ya fácil buscar la proporción de este "número áureo" en el mismo triángulo perfecto.
.
BAJO ESTAS LÍNEAS: De nuevo la imagen mía junto a la pirámide se Saqara, aunque esta vez la hemos coronado con el "triángulo perfecto" (en amarillo). Bajo esta, vemos el modo de hallar las raices cuadradas simplemente utlizando la hipotenusa como siguiente cateto en un triángulo que siempre tenga (a)=1. Consecuentemente, en el primer caso (b) será = 1; en el segundo (b)=Ѵ2; el tercero (b)=Ѵ3; el cuarto (b)=Ѵ4; el quinto (b)=Ѵ5; el sexto (b)=Ѵ6; y etc.. Partiendo de estas proporciones y desde las ya establecidas del triángulo perfecto, expondremos las razones de la "sección áurea" nacida desde aquellos.
.
A)- Así, en el triángulo "1", "1" ,Ѵ2 (negro); sus proporciones son:
a:b=b/a=1 ; a/c = 1:Ѵ2 = Ѵ1/2 ; (a+b):c = (1+1):Ѵ2 = Ѵ2
.
B)- En el siguiente que es (rojo) "1", "Ѵ2", "Ѵ3" las proporciones son
a:b = 1/Ѵ2 = Ѵ1/2 ; a:c = 1/Ѵ3 = Ѵ1/3 ; b:c = Ѵ2/Ѵ3 = Ѵ(1/1,5)
.
C)- El de color azul que tiene "1", "Ѵ3", "Ѵ4", lleva estas proporciones:
a:b = 1/Ѵ3 = Ѵ1/3 ; a:c = 1/Ѵ4 = 1/2 ; b:c = Ѵ3/Ѵ4 = Ѵ3/4
.
D)- Finalmente el verde contiene "1", "Ѵ4", "Ѵ5", y se proporciona como:
a:b = 1/Ѵ4 = 1/2 ; a:c = 1/Ѵ5 = Ѵ1/5 ; b:c = Ѵ4/Ѵ5 = Ѵ4/5
Pero a su vez este triángulo verde guarda la sección áurea en razón:(c:b) + (a:b) = (Ѵ5:2) + (1/2) = 1,118033989 + 05 = 1,618033989... = 
.

.
Como hemos podido ver, el triángulo último en la "serie de hipotenusas" que hemos creado, contiene plenamente la fórmula de "fi"; ya que al ser sus LADOS (a)=1; (b)=Ѵ4; (d)=Ѵ5 . (a/b)+(d/b) = 1,618033989... (número de la "sección áurea", que se dibujaría de este modo -al menos en mi opinión-). Aunque la misma proporción podremos escribirla también con el triángulo siguiente:
,
BAJO ESTAS LíNEAS: Dibujado sobre la clave de la iglesia de Pampliega (Burgos) otro modo de representar "fi" (en mi idea); triangularmente y cuando los lados son (a)=1; (b)=2 ; (c)=Ѵ5 .
.
Siendo así que:(a/b) + (c/b) = = 1,618033989...
Por su parte este triángulo entero es igual a:
a+b+c = 2 + 2
. Finalmente, sobre el mismo triángulo, en la foto y en líneas amarillas; hemos representado lo que significaría "fi"
 = (½ a) + (½ b) = (½) + (½ Ѵ5) = 0,5 + 1,118033989... =1,618033989...
.

.
BAJO ESTAS LíNEAS: Dibujado también sobre la clave de la iglesia de Pampliega (Burgos); los dos triángulos sagrados de Egipto, de los cuales procede la Sección Áurea y la afinación llamada pitagórica; basada en los intervalos: 1/2, 2/1 ; 3/4, 4/3 ; 5/4, 4/5 ; 5/3, 3/5 .
.

Hipótesis arquelógica sobre las primeras temperaciónes y escalas musicales (capítulo I)

1.- BREVE EXPOSICIÓN DE LAS TEMPERACIONES EN CHINA
.

Iniciamos aquí nuestro estudio acerca de los temperamentos en la Antigüedad, donde trataremos sobre la creación de la escala musical, las notas y la afinación de los instrumentos. Y lo comenzaremos mencionando algunos aspectos en la música oriental, aunque el trabajo nuestro tratará preferentemente de la afinación "mediterráneas" u "occidentales". Todo lo que significa que la música china -o la de la lejana Asia- quedará al margen de lo que trataremos comunmente en nuestros planteamientos arqueológicos y filosóficos acerca de la historia en las escalas musicales. Puesto que en el presente estudio nos hemos fijado como finalidad descubrir más sobre el significado de los orígenes en la música Europea y mediterránea. Partiendo desde la de Egipto y de Babilonia, pasando posteriormente a la judeocristiana y la grecorromana, para llegar a comprender finalmente las escalas más modernas.
.

Pese a ello, recogeremos un breve esbozo acerca de la arqueología musical en China, basándonos en los estudios de Ma. Dolores García-Borrón, y en especial en su tésis doctoral "Historia de las artes y espectáculos en China". Un trabajo, que trás estudiarlo, se observará cómo resulta indudable que la música china, la egipcia, babilónica -o la griega- parecen tener unos "parámetros" para hallar sus temperamentos muy similares. Incluso en algunos casos, unas dataciones en la aparición de las escalas musicales que se acercan mucho en fechas. Tanto que hacia el 1500 a.C. podemos leer en historias escritas del imperio asiático, donde mencionan cómo el músico, filósofo y matemático Ling Lung, usaba métodos muy similares a los egipcios y a los posteriormente ultilizados por Pitágoras, para encontrar una escala armónica basada en proporciones de Quintas (en capítulos posteriores explicaremos qué es la Quinta y su método de hallarzgo en la Escala -para quienes no lo conozcan-). Asímismo, hasta el tiempo del referido Ling Lung, se creee que el número de notas musicales en China era un total de cinco, creando musica pentatónica; aunque en estos años pasarían a siete los tonos y porteriormente a doce sonidos (como la occidental "común").
.

Legendariamente, y según la tradición china, la música comenzó en el siglo XVII a.C., desde que el emperador Huang Di (1695-1597 a.C.), envió al mencionado sabio Ling Lung al Oeste, con el fin de crear la flauta de bambú que imitara el canto de las aves. Un dato de gran importancia por cuanto refiere la venida al Oeste de aquel matemático con el fin de estudiar la creación de la escala. Pudiéndonos hacer suponer que las notas musicales llegaron hasta la civilización china en este tiempo, importadas desde lo que fue para aquellos Occidente (Asur, Babilonia o de zonas en contacto con Egipto). Una hipótesis que exponemos como muy personal y nuestra, ya que nos resulta extraño el recuerdo y la memoria del citado viaje de Ling Lung; viniendo hasta "el Oeste" para buscar la temperación armónica. Considerando que no resulta una idea tan extraña creer que tales notas fueran traidas a China desde Mesopotamia en el siglo XVI a.C., debido a que el número de tonos "creado" por Ling Lung fué el mismo que en las culturas cercanas al Mediterraneo usaron (y que era el de doce).
.
BAJO ESTAS LINEAS: Un grabado japonés en el que vemos músicos en la corte de Tokio (autor Utagawa Kunisada, hacia 1850). La falsa creencia de que la música oriental es pentafónica se observa en cuanto se escuchan las melodías cantadas o las okarinas y múltiples flautas japonesas (como el maravilloso shakuhachi que vemos tocar en el grabado de la derecha). Instumentros y voces que se temperan sin un orden siquiera cromático y en los que se usa el cuarto y hasta el octavo de tono de manera controlada (como sucede en el Flamenco y en gran parte de la música oriental). Pese a ello, conviven junto a estas formas melódicas que pueden crear decenas de notas en una misma escala, algunos intrumentos que como el Shamisén, contiene una base puramente de cinco notas.
.

.
Por lo demás, el 12 era la cifra sagrada babilónica, tanto que aquella civilización contaba en sistema duodecimal (por docenas) y todo lo medía en relación a lo sexagesimal o al doce. Pero su vez los pueblos semitas y de origen mesopotámico, tenían unas semanas de siete días y dividían el 12 astralmente en en dos cilclos (uno de 7 y otro de 5). Ello porque su calendario fue lunisolar y como tal la base ha de estar en ambos números en relacion a los giros planetarios. El 7, porque divide los ciclos de la Luna que tiene periodos muy cercanos al femenino; contando con 29,53 dias (como luz reflejada del Sol); o con 28 días (como medida en las mareas). De lo que conformaron las semanas de 7 días que por 4 suman 28 y que es lo más aproximado al mes lunar (el latín "mensis" -que coincide con los ciclos de fertilidad de la mujer-). Por su parte el 5 y el 10 son los números del Sol, por cuanto su año aproximado es de 365 días; lo que supone 73 x 5, un número que en verdad se concebía como los grados de la circunferencia (360º) más 5. De cuanto explicamos, para los calendarios lunisolares mesopotámicos el 5 y el 7 eran imprescindibles, de lo que la cifra sagrada babilónica se entiende que fuera el 12 (no solo por ello sino sobre todo por la utilidad del sistema duodecimal para trabajar la circunferencia). Pero que dividido en 7 + 5 tenía un significado astral, siendo su organización igual al orden de las notas musicales (7 naturales y 5 sostenidasque conforman los 5 tonos y los 7 semitonos ) -esta relación plena entre los planetas y la Escala, la iremos viendo en posteriores capítulos-.
.

Pese a ello, tampoco sería definitivo el hecho de que Ling Lung impusiera una escala de doce notas, para considerar que la importó desde Mesopotamia. Dado que -como veremos mas adelante- este número de tonos es el que naturalmente "sale" al temperarse del modo armónico por Quintas (lo que ya estudiaremos como se hace). Aunque un hecho que resulta una coincidencia inexplicable entre las afinaciones china, babilónica, egipcia y griega -más que ese número final de 12 notas-, es el método usado, dividiendo las Escalas de una forma igual. División y modo de temperar que incide en que haya una cantidad de sonidos que terminen componiendo los 12 (5 tonos y 7 semitonos) -todo cuanto iremos exponiendo y explicando a lo largo de las primeras partes de este estudio-. Por lo demás, el sistema duodecimal, tal como dijimos anteriormente era el que precisaban los astrónomos (fundamentalmente los asirios) y su explicación matemática es muy simple, naciendo el método sexagesimal para trabajar en Grados. Ya que la división de la circunferencia en 360º, hecha ya a principios del tercer milenio a.C. -atribuida por unos a los babilonios y por otros a los egipcios-; obligaba a tener como base el 6. Todo lo que conformaba la técnica y el modo sexagesimal para poder guiarse en el desierto, medir bien las distancias y ser capaces de estudiar el cosmos. De lo que precisaron una cifra que fraccionase perfectamente el 360, y que precisaba operar de 6 en 6, puesto que el 10 o el 5 no son fraccionarios naturales de 360.
.
BAJO ESTAS LÍNEAS: Un Ukiyo-e del grabador japonés Utagawa Kunisada (hacia 1850) en el que vemos una tañedora de Shamisén. Tal como decimos, este instrumento es muy precario en su manejo, afinación y hasta en el sonido (habida cuenta que la caja de la "guitarrita" o "pandura" es literalmente un tambor). Pese a temperarse comunmente en pentafónico, se usa para acompañar cánticos cuyas melodías carecen de afinación occidental y cuyos tonos pasan por 1/4, 1/8 y hasta el 1/16 de nota (controlada).
.

.
De todo ello surge el sistema duodecimal, tan impuesto en Asiria, que allí el doce sustituyó al diez. Tanto era así, que los sumerios contaban hasta doce con los dedos de la mano, por el procedimiento de llegar a diez con las dos palmas abiertas, a once con un puño cerrado, siendo doce los dos puños cerrados -un sitema tan impuesto entre las culturas semitas, que desde los árabes hemos heredado nosotros como determinados artículos áun se cuentan por docenas en el comercio-. Por todo lo anteriormente expuesto y dado que el número de sonidos musicales de otras escalas en culturas cercanas a China, son muy distintos a siete más cinco (como por ejemplo, los veintidós de la Octava védica, en la India). Pudiéndose demostrar que en Egipto y en Babilonia fueron ya en el II milenio a.C. doce las notas. Es posible también mantener la hípótesis de que la mencionada escala de Ling Lung (sabio ministro del siglo XVII a.C. chino), quizás llegó hasta este país en instrumentos llevados allí por mercaderes venidos desde Asiria o de zonas con gran influencia egipcia (Asia Menor o Arabia). Unos hechos que quizás se recogen en la famosa narración que nos recuerda como aquel sabio trajo los temperamentos trás un largo viaje hacia el Este.
.

Esta historia que nos relata el principio de la música en China; según García-Barrón se trataría tan solo de una leyenda y posiblemente de origen mucho mas antiguo. Así la vemos también nosotros, pues en nuestra opinión quizás sea una historia ancestral, nacida de épocas muy anteriores -cuando aún la escala era de cinco notas en China-. Narración que quizás se reescribió al transformarse finalmente la Escala en una octava de doce sonidos (hacia el siglo XVII a. C.). La antigüedad de la fábula se observa claramente al principio de la historia, cuando nos habla de una época ancestral; mencionando una etapa donde había aún gran unión entre la música y la caza. Refiriéndo que a Ling Lung le encarga el Emperador que crease la flauta que imitara del canto de los pájaros. Con ello, hemos de entender que no solo se refiere a la belleza sus sonidos, sinó que la leyenda tiene un sentido mas cinegético que artístico. Pues comprobado está que los reclamos de los cantos ornitológicos, fueron los primeros instrumentos musicales muy depurados, habida cuenta que eran la mejor ayuda para el hombre en el ejercicio de esta primegina profesión de cazador.
.
Pero sin lugar a dudas, estos reclamos de caza debieron ser el origen del estudio para la comprensión de los tonos en las flautas, imitando perfectamente gracias a ellos el sonido de las aves. De lo que continuando con la historia de Ling Lung y con la arqueología musical china, la mencionada autora mantiene que el origen de los instrumentos en aquella civilización puede documentarse en unos siete mil años de antigüedad. Lo que hace pensar que esta leyenda sobre la creación de la música datada unos tresmil setecientos años atrás, se refiera solo a la historia de la escala de doce notas. Es decir, que antes de Ling Lung ya hubo una "Octava" de cinco sonidos y muy característica de China, mientras que el sabio habría traido del Oeste una con siete tonos más. Cuanto exponemos se acredita con el hallazgo de múltiples instrumentos pentafónicos y que pueden fecharse desde el 5000 a.C., tales como son: Flautas de arcilla ("xun"), carrillones de piedra ("quinq"), campanas carrillón ("zhong"), y las zamponas o flautas de pan ("cheng").
.
BAJO ESTAS LINEAS: Del mismo autor que antes, un grabado con una cortesana tocando el xilofón (Utagawa Kunisada hacia 1850). Observemos que el instrumento tiene 24 notas (o teclas) lo cual expresa claramente que se trata de un temperamento basado en doce notas de las cuales contiene dos Escalas. Ello para interpretar igualmente música japonesa.
.

.
Por su parte y curiosamente, entra en la escena musical china a fines del siglo XVII a.C., un nuevo instrumento tipicamente egipcio, anatolio y babilonio, como lo es la cítara (allí con cuerdas de seda). Liras, formix o arpas que a nuestro parecer pudieron llevar hasta allí esta nueva temperación de doce notas, sustituyendo a la música pentatónica. Por esta aparición de la cítara en China, justo en el momento que allí da comienzo de una Escala nueva con doce notas; puede deducirse que aquel instrumento llevó el nuevo temperamento a Asia hacia el 1600 a.C. De lo que este puede ser un argumento más que suficiente para poder suponer que el dodecafonismo (cromatismo) llegaría a China desde Asia Menor o de Anatolia y con estas liras, tan tipicamente mediterráneas.
.
Además, la cítara fué el instrumento mas usado por los anatolios y el preferido de los hititas (quienes durante la época que hablamos eran los "dueños" de la actual Turquía). Civilización de Hattusa que extendió sus dominios hasta las proximidades del Nilo y de Babilonia -antes del descubrimiento del nuevo metal con el que cambiaron la historia del mundo sobre el siglo XIV a. C.-. Realizando incursiones los hititas hacia el Sur y el Este, invadiendo reinos como el faraónico; hasta el punto de algunos historiadores afirman que crearon su propio Imperio del Nilo con capital en Avaris sobre el siglo XVIII (según teoría común por la cual el reino hicso procedería de Anatolía -idea discutida por muchos, que consideran a los hicsos como tribus procedentes de Siria-). Sea como fuese, el imperio de Hatti -como llamaban los egipcios a los hititas- fue tan fuerte, que a través del mundo Escita envió sus influencias hasta China; y de la misma forma que introdujeron el hierro en el corazón de Asia (desde Anatolia), pudieron importar las cítaras y con ellas, la temperación babilónico u egipcia de doce notas.
.
Por su parte, mantiene García-Borrón, que la creación de los sonidos por el sabio ministro Ling Lung se hizo por medio de cañas de igual grosor, cortadas a distancias distintas (en un total de doce). Sobre ello y en nuestra consideración, debemos añadir que indicaría cómo la leyenda no se corresponde con una verdad histórica. Ya que es muy difícil temperar por medio de cañas a distintas alturas, dado que las notas deben ajustarse no solo a una longitud proporcional perfectamente cortada, sinó también al grosor interior del tubo. Por lo que calcular una escala primera de esta forma es casi imposible, pues una pequeñísima desigualdad milimétrica de corte o de sección -y (sobre todo) cualquier nudo interior de la caña- modifican el tono. Por cuanto exponemos, nos resulta muy difícil pensar que el origen de la escala, se buscara con una "flauta de Pan" -o con tubos cortados a modo del instrumento llamado en China Cheng o Sho-; ya que como decimos, cualquier modificación en el perímetro interior de aquellos (o en su corte y sección) pueden producir notas muy distintas. Por el contrario, la forma mas sencilla de buscar los sonidos o de afinar la Escala es hacerlo sobre una cuerda tensada y larga; atada en un soporte con buena resonancia, algo que puede crear y realizar un simple fabricante de arcos. Una vez tenido ese "cable" largo y tenso, bastara ir tapando proporcionalmente una parte de aquel, para ir temperando o averiguando una escala proporcional y armónica (este instrumento de afinación es el que entre los pìtagóricos se llamó el "monocordo").
.
BAJO ESTAS LÍNEAS: Tañedoras de Shamisén (una con arco y otra con plectro) bajo la cantante que lee depié y en el libro, la melodía y poema; por el grabador japonés Yoshinobu (hacia 1770). Como expresamos, la complejidad de la música oriental consiste en la convivencia de melodías e intrumentos ancestrales (como esta guitarrita tan común a las geishas), junto a la inclusión de métodos, objetos, formas e influencias llegadas desde Occidente desde los siglos XVIII y XIX.
.
.
Quizás por la razón antes expuesta sea por lo que García-Borrón afirma que los "doce liu" (o las doce notas de Ling Lung) no estaban bien reguladas, aunque partían de una progresión de quintas -algo que no entendemos muy bien en toda esta historia, pues si se progresa en Quintas, veremos que es imposible no temperar bien-. Aunque asimismo hay otros autores que consideran que las notas (o "liu") de este músico no eran doce sinó solo cinco e incluso que su afinación coincidía con los intervalos existentes entre las teclas negras del piano (mas tarde podremos estudiar cómo y por qué en la afinación de doce notas quedan de forma natural cinco sostenidos, que generan un pentafonismo con plenamente sonido oriental -correspondiéndose con las teclas negras del piano-). Desconocemos realmente si fueron cinco o doce, y aún mas los tonos de Ling Lung; tanto como cual era el fallo de afinación del que nos habla García-Borrón; pero mucho nos hace sospechar que el intento de realizar por medio de cañas una temperación ya indica que el modo no era correcto ni viable. O lo que es lo mismo: Que posiblemente se trataba de un sistema importado desde una nación -o civilización- extranjera y por ello no comprendido en su totalidad. Con lo que podemos deducir que la historia de Ling Lung "inventando" los doce tonos creando una flauta de pan con tubos graduales, quizás nos indica realmente que no conocían en verdad la forma exacta para temperar la octava aunque la usaban (porque tal y como decimos, se hace casi imposible descubrir las notas con cañas -cosa muy diferente a fabricar la flauta de Pan, una vez conocido el sonido de las 12 notas-).
.
Finaliza esta leyenda dando Ling Lung, un significado cósmico y social a las doce notas, siendo cada una de ellas el símbolo de las doces castas de la China de entonces y teniéndose a primer tono como representación del Emperador, del cual surgen todos los demás (adjudicándoles un sentido simbólico y celeste también a esos sonidos -algo muy similar a lo que sucedió en Egipto, Babilonia y Grecia-). Por su parte, y a nuestro parecer, el hecho de no haberse resuelto correctamente una temperación de doce notas basada en Quintas (tal como alude García-Borrón), nos lleva a afirmar que la afinación fue importada desde Occidente pero sin llegar a ser entendida plenamente. Tal como recoge la leyenda al decirnos que Ling Lung creó su Escala el Oeste, viajando hasta la puesta del Sol (para realizar allí la temperación). Por lo que consideramos que la teoría armónica cromática pudo estar mal interpretada en la China del XVII a. C., porque no fuera una teoría resuelta ni inventada aún allí. Pues como veremos durante esta obra que ahora empezamos, la resolución de la afinación en doce notas -una vez bien comprendida-, puede hacerla alguien sin apenas conocimientos matemáticos (bastándole una cuerda tensada). Llevándonos todo ello a concluir definitivamente que podríamos obviar como en esta época legendaria de Ling Lung llegaron a China instrumentos venidos desde Asia Menor y de Egipto. Liras y arpas basadas en sistemas de doce notas, que muy posiblemente copiarían en China, pero sin resolver correctamente sus distancias de afinación. De cuanto se conservaría así la fábula del sabio tanto como la falta de resolución armónica; que destacan los historiadores al hablar de las notas que creó este ministro y músico del emperador del siglo XVII a.C..
.
.
COMENTARIO A LAS IMÁGENES: Arriba, bajorrelieve neohitita de Katerpe (fortaleza); procesión con músicos fechada en el siglo VIII a.C. (pieza del Museo Arqueológico de Estambul -al que agradecemos nos permita divulgar su foto-). Como podemos observar en el ortostato, al frente va un flautista, trás este un ciratista de lira, luego un arpista y al final un percusionista (con un pandero). Los instrumentos tienen por su orden: La lira que vemos en el segundo, seis cuerdas y se regula claramente por tensión de clavijas. Tras ello hay un arpa pequeña, que se afina por alturas (o longitud) que porta ocho cuerdas. Evidentemente, por la forma de marchar, el lugar de donde procede la pieza y la escena, sabemos que se trata de un "modo" musical "frigio", heredado claramente de los hititas.

ABAJO: Relieve hitita procedente de Alaca-Höyuc y fechado en el siglo XIV a.C; en este se observa un tocador de pandura (laud), junto a un sacerdote u oferente que le entrega una oveja (del Museo de las civ. de Ankara, al que agradecemos nos permita divulgar la imagen). La importancia de la escena consiste en que la pandura está trasteada. Un hecho que no habíamos observado en otra escultura más antigua; desconociendo si este ortostato hitita que traemos a imagen se trata de la escultura más antigua existente en la que se representan los trastes de un laud (o instrumento semejante a la guitarra). De hecho la observación es personal, aunque no nos extrañaría que otros se hubieran apercibido del mismo detalle de tanta importancia. Puesto que hay quienes llegan a manifestar que hasta El Renacimiento no se ponen trastes a los instrumentos de cuerda. Por lo demás esta pandura trasteada que vemos en la fotografía y con unos tresmil quinientos años de antigüedad, goza de una afinación que parece "decafónica". Habida cuenta que no solo en la caja hay diez marcas, sinó que se cuentan unos veinte trastes en el instrumento, lo que hablaría de una división en diez notas de la música. Aunque muy difícil es saberlo, puesto que una de las manos que tañen el intsrumento tapa todo el final de su mástil.
.
.
Por último, comentaremos que García-Borrón, afirma también que la temperación moderna (Bien Temperada) se descubrió unos años antes en China; precediendo decenios a la misma afinación inventada en Occidente. Para lo que argumenta que el famoso matemático chino príncipe Zhu Zaiyu (1536-1614) empleó ya en 1584 la fórmula moderna de afinar los instrumentos basada en una progresión geométrica nacida de dividir la octava en doce tonos (2 elevado a 1/12; o lo que es lo mismo "raiz 12" de 2). Un método que se denomina afinación Bien Temperada y que se usó fundamentalmente tras J. S. Bach en todo Occidente. Por la que se realizó tras una división progresiva del diapasón partiendo los doce sonidos en base a una proporción igual y aritmética. Continuando la autora exponiendo que el primero en aplicar tal progresión en la distancia y division de los trastes en Europa fué Marín de Mersenne (1588-1648), quien en 1636 desarrolla la ecuación que lo soluciona, pero que mas de cincuenta años antes, esta ya se usaba en China. Por nuestra parte solo añadir que el descubrimiento de la raiz 12 de 2 o (bien dos elevado a un doceavo) no es de Mersene, sinó que se atribuye en occidente a Simón Stevin (1548-1620), coetaneo del mencionado príncipe chino Zhu Zaiyu. Así mismo se tiene al holandés Stevin como el creador de la división de la octava en doce notas, cuya distancia entre una y otra nace de la aplicacion de este número nacido de la raiz de 2, llamado "Lambda". 
.
Por su parte, la ecuación de Marin de Mersene que García-Borrón menciona, no fué en relación a la raiz cuadrada de un doceavo (como escribe), sinó la llamada ley de la cuerda vibrante, que resuelve la frecuencia de vibración en razón al inverso de su longitud y la ráiz cuadrada de la sección o densidad lineal de la cuerda. Para completar mas datos, la afinación temperada ya llevaba antes de Stevin estudiándose por muchos científicos y musicos del siglo XVI, entre los que destacó con gran brillo en el intento de su resolución en español Francisco de Salinas (1513-1590). Tanto, que un experto y especialista como es Javier Goldáraz Gaínza en el capítulo IV de su magnífico libro "Afinación y temperamentos históricos", le dedica las siguientes palabras: "Es sorprendente que ningún historiador de la música español haya reivindicado para Salinas, si nó la invención, al menos la primera exposición exacta del temperamento igual. El propio Salinas se atribuye esta primacía ..." en 1577. Tras ello, este interesante autor cita como además de Salinas continuaron con el trabajo para conseguir la temperación igual, V. Galilei, y Zarlino hacia 1588, para finalmente realizarlo el mencionado Stevin en 1600.
.
.
De todo ello podemos deducir al menos, que el dato dado por García-Borrón que atribuye a Marín de Mersenne la creación de "Lambda", o lo que es lo mismo, de la afinación Bien Temperada (las notas modernas) no es correcto. Realmente, desconocemos si el príncipe chino tuvo contacto con Simón Stevin (o viceversa), y aún menos, si el aristócrata oriental tomó esta división de la octava, de los instrumentos llegados desde el otro lado del Mundo, desarrollando una teoría venida con los nuevos cordófonos occidentales cargados de trastes (algo que comenzó a ponerse en los mástiles de instrumentos de cuerda en el siglo XVI, que hasta esta época carecieron por lo común de divisiones). O bien, si por el contrario, la fórmula de la "raiz doceava" de 2 viajó desde China a Holanda e Italia (lugar de origen de los Zarlino, Galilei y Stevin) o si aquel príncipe , participó en todas las corrientes culturales y matemáticas de la época occcidentales, que estudiaban la afinación en el Renacimiento europeo.
.
Pero para admitir la tesis de García-Borrón dando como inicio de la afinación Bien Temperada a China, habría de suponerse que hubo una coincidencia científica (algo que tanto ocurre) desarrollando una igual fórmula ambos sabios en distintos lugares e igual época. Más de ser así y haberse creado la afinación Bien Temperada en Asia, lo extraño es que ni la música china ni los compositores chinos hayan destacado en esta música cromática de 12 notas, mientras en Occidente al cambiar el sistema de temperación nacieron compositores tales como Bach, Häendel y un gran etc. La Historia nos obliga dilucidar, que la creación del cromatismo musical tanto en temperación antigua (pitagórica) como en la moderna (Bien Temperada) procede del area de Asia Menor, del Mediterraneo o de la Europea. La primera en época egipcia, babilonica o griega (en la Antigüedad), y la segunda, con la temperación igual, parece un producto occidental nacido del Renacimiento. Y es que se nos plantean dos dudas para atribuir ambos tipos de temperación a China: La primera sería la de que muy poca música china encontramos en doce notas debido a estos cambios de afinación ni en el siglo XVII a C., ni en el XVII (d. C.). La segunda, es que mientras en Europa la afinación bien temperada surge tras medio siglo de teorías e investigaciones musicales y debido a muy diferentes teorías de muy distintos sabios; parece que en China fué descubierta por un solo individuo, de modo improvisado y sin una investigación común con varios músicos y matemáticos. Lo que nos resulta difícil encajar históricamente, dada la complejidad de las temperaciones, y su sucesión que siempre vino evolucionando y variando por motivo de la creación de nuevos instrumentos, nuevas músicas y nuevas tendencias en la composición y la interpretacion.
.
Por su parte, en lo que respecta al nacimiento de Bach, o Häendel, creemos firmemente que estos compositores fueron fruto del cambio de Temperaciónes en su época y de una compresión muy distinta de la música (algo que ya nadie podríamos tener), pues son figuras surgidas en una transición cultural, en la que se comprendía una nota como una Quinta, una Cuarta o una Tercera (originada de una fórmula matemática) para pasar también a ser concebida en la nueva afinación, como un doceavo de una progresión geométrica del diapasón (todo esto lo explicaremos y estudiaremos detenidamente en nuestro trabajo, de forma sencilla y simple, tanto que podrán comprenderlo, aún quienes carezcan de conocimientos matemáticos y musicales). Esa doble visión y división de lo que era una Escala que vivieron los músicos de la Era de J.S.Bach, creemos que fué uno de los motivos que engendraron ese gran genio y padre de la música "clásica" (y de muchos de los que le rodearon). Algo que fué diluyéndose conforme el artista conmprendió como normal que matemáticas y música se segregasen; y que una Quinta, ya dejase de tener un significado ecuacional ( a mas de uno musicológico) para pasar a ser una distancia equitativa aritmética. En el presente estudio intentaremos integrar el concepto de música y matemática, y comprender cómo la importancia de un concepto abstracto y exacto de la armonía es importante, tanto como para poder determinar que lo bello, lo armónico y lo sublime sí puede tener una medida justa y universal. Y si no puede determinarse que exista lo inarmónico (puesto que lo feo o descompuesto es criterio subjetivo de cada individuo o cultura) sí puede determinarse que exista lo armónico y bello para todos; es decir: La Armonia Universal (igual que hay una verdad matemática o física, al menos para cada época).
.
ABAJO: El autor de estas lineas tocando en público en Tokio, en concierto para el presidente de Sunwa Corporation -Roppongi Hills 2007-.
.